* 논문 링크
https://www.sciencedirect.com/science/article/pii/S0925231222000522
SRDiff: Single image super-resolution with diffusion probabilistic models
Single image super-resolution (SISR) aims to reconstruct high-resolution (HR) images from given low-resolution (LR) images. It is an ill-posed problem…
www.sciencedirect.com
* 저널 정보

SRDiff는 작년 논문으로 Neurocomputing에 발표된 논문이다. Neurocomputing이라는 저널은 처음 들어보는데 찾아보니 엄청 영향력 있는 저널은 아닌 것 같다.
* 본 논문 읽은 이유?
초해상화 관련 연구를 진행하고 있기에 읽어 보았다.
디퓨전 관련 내용이라 그런지, 아니면 내가 부족해서 인지 ,,, ㅜㅜ 둘다 맞겠지만? 이해하는데 어려웠음..
* SRDiff 는 무엇을 위한 모델?
- 기존 SISR method의 문제를 해결하기 위함이다.
- SISR method의 문제로는 아래 3가지 가 있다.
1. Over-smoothing
2. Mode collapse
3. Large footprint
* SRDiff 간략한 설명
- T-step diffusion model로 이루어졌으며, 이는 Diffusion process와 Reverse process 두 과정을 가짐
- High Resolution의 직접적인 예측 대신 residual 예측을 적용함
- 이는, High Resolution img $x_{H}$와 upsampled Low Resolution img $up\big(x_{L})$ 사이의 차이를 예측하기 위함
[Diffusion process]
- $x_{0}$를 Gaussian noise $\epsilon$를 점점 추가하면서 Gaussian 분포를 가진 latent variable $x_{T}$로 변환$$x_{t} \big( x_{0}, \epsilon\big) = \sqrt{ \overline{ \alpha_{t}}} x_{0} + \sqrt{ 1-\overline{ \alpha_{t}}}\epsilon, \epsilon \sim N \big(0,I\big) $$
[Reverse process]
- $\epsilon_{ \theta}$에 의해 결정됨
- $\epsilon_{ \theta}$ 는 RRDB 기반 Low Resolution Encoder $D$를 가진 conditional noise predictor임
- $\epsilon_{ \theta}$를 사용한 T-step을 무한의 수만큼 denoising을 반복하면서 latent variable $x_{T}$를 residual img $x_{r}$로 변경
- Super Resolution img는 residual img $\widehat{x}_{r}$를 upsampled Low Resolution img $up\big(x_{L})$ 에 더함으로써 재구성됨
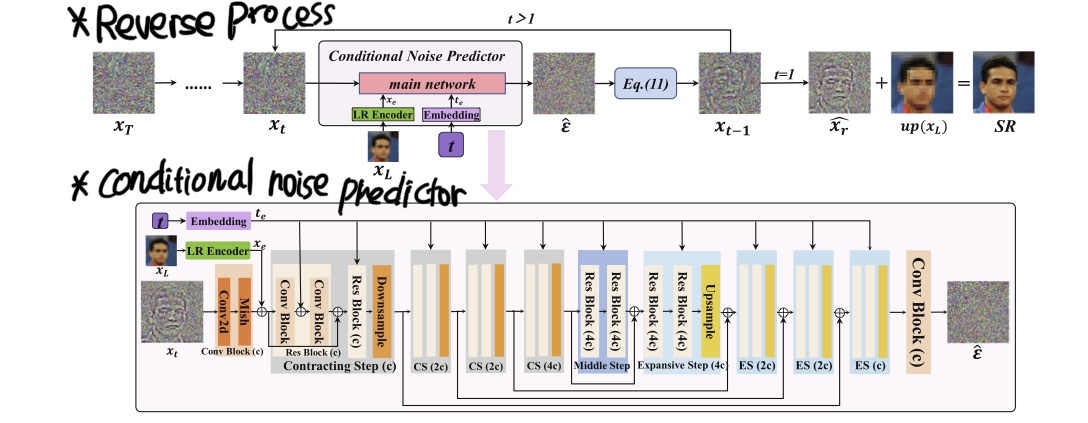
[Conditional Noise Predictor $\epsilon_{0}$]
- 목표 : Low Resolution image 정보에 따른 각 diffusion timestep에 더해진 noise $\epsilon$을 예측하는 것으로 아래 방정식을 따름
$\min_{ \theta } L_{t-1}(\theta) = E_{ x_{0}, \epsilon ,t} \begin{bmatrix} \| \epsilon - \epsilon_{0} \big( \sqrt{ \overline{ \alpha }_{t}} x_{0}+ \sqrt{1-\overline{ \alpha }_{t}} \epsilon ,t \big) \|^{2} \end{bmatrix} $
$ \mu _{ \theta } ( x_{t},t ) : = \frac{1}{ \sqrt{ \alpha _{t} } }( x_{t}- \frac{ \beta _{t} }{ \sqrt{1- \overline{\alpha} _{t} } } \epsilon _{ \theta }( x_{t},t ) )$
$\sigma _{ \theta } ( x_{t},t ) : = \widetilde{\beta}_t^\frac{1}{2}, t \in \big\{T, T-1, \cdots ,1 \big\} .$
- U-Net을 main으로 사용
- 인풋은 3-채널 $x_{t}$과 diffusion timestep $t$, LR 인코더의 출력을 사용함
- $x_{t}$는 2-D 컨볼루션 블록과 레이어, Mish 활성 함수를 통한 hidden state로 변형됨
- LR 정보는 그 다음 2-D 컨볼루션 블록에 의해 hidden state 출력과 함께 결합함
- 본 논문은 transformer안에 제안된 sin positional encoding 을 사용하면서 timestep $t$를 timestep embedding $t_{e}$으로 변형함
- 2D 컨볼루션 블록의 hidden state와 $t_{e}$는첫번째 contracting step의 residual 블록에 공급됨
- 이러한 과정들(contracting path, middle step, expansive path, 마지막 2D 컨볼루션 블록)을 통해 $t$ diffusion step에 추가된 노이즈가 예측됨
- 모델 크기를 줄이기 위해 두번째와 네번째 contracting steps의 channel size를 두배로 하고 각 contracting step안에 있는 feature map의 spatial size를 반으로 함
- 마지막으로 2D 컨볼루션 블록은 예측된 노이즈로써 timestep $t$의 $\widehat{ \epsilon }$을 생성하기 위해 적용됨
- 예측된 노이즈 : 아래 방정식을 따라 $x_{t-1}$을 회복함으로써 사용된 예측 노이즈
$P_{\theta}(x_{0}, \ldots , x_{T-1}|x_{T}):= \prod_{t=1}^T P_{\theta} (x_{t-1}|x_t)$
$P_{\theta}(x_{t-1}|x_{t}):=N \big(x_{t-1};\mu_{\theta}(x_{t},t),\sigma_{\theta}(x_{t},t) ^{2}I \big) $
$\min_{ \theta } L_{t-1}(\theta) = E_{ x_{0}, \epsilon ,t} \begin{bmatrix} \| \epsilon - \epsilon_{0} \big( \sqrt{ \overline{ \alpha }_{t}} x_{0}+ \sqrt{1-\overline{ \alpha }_{t}} \epsilon ,t \big) \|^{2} \end{bmatrix} $
$ \mu _{ \theta } ( x_{t},t ) : = \frac{1}{ \sqrt{ \alpha _{t} } }( x_{t}- \frac{ \beta _{t} }{ \sqrt{1- \overline{\alpha} _{t} } } \epsilon _{ \theta }( x_{t},t ) )$
$\sigma _{ \theta } ( x_{t},t ) : = \widetilde{\beta}_t^\frac{1}{2}, t \in \big\{T, T-1, \cdots ,1 \big\} .$
* LR Encoder
추후 작성 예정
* Training and Inference
추후 작성 예정


