728x90
머신러닝에 필요한 기초적인 수학 공부를 하기 위해 "선형대수와 통계학으로 배우는 머신러닝 with 파이썬" 이라는 책을 읽고 블로그에 요약해보고자 합니다. 오직 제 개인적인 공부 공간으로 사용할 목적으로 포스팅을 할 예정이니 자세한 내용이 궁금하신 분들은 아래 표지 책을 구매하여 공부하시길 바랍니다.
이전 포스팅 >>>>> [STUDY/인공지능] - [ML 책] 고유값, 고유벡터, 고유값분해
[ML 책] 고유값, 고유벡터, 고유값분해
머신러닝에 필요한 기초적인 수학 공부를 하기 위해 "선형대수와 통계학으로 배우는 머신러닝 with 파이썬" 이라는 책을 읽고 블로그에 요약해보고자 합니다. 오직 제 개인적인 공부 공간으로 사
chaeso-coding.tistory.com
[특이값 분해 Singular Value Decomposition]
- 정사각 행렬 대상(고유값 분해)이 아닌 $m \times n$행렬로 일반화 시킨 것
- 행렬의 차원 축소를 위한 도구로 쓰임
- PCA같은 차원 축소 분야에서 많이 쓰임
차원 축소?
1. 데이터 전체 공간의 차원보다 낮은 차원으로 적합시킬 수 있는 기존 행렬의 차원보다 낮은 차원의 공간을 찾는 것
2. 행렬 $A$가 $p$차원이라 했을 때, $A$를 $d$차원 $(p>d)$로 축소한 행렬을 $B$라고 하면, 특이값 분해는 차원 축소 행렬 $B$를 찾는데 사용하며 $d$차원은 직접 정할 수 있음
- 행렬 $A$의 크기가 $n \times p$라면 $p$차원에 $n$개의 점 존재한다고 생각할 수 있음
- 행렬 $A$에 대한 차원 축소란 $n$개의 점을 표현할 수 있는 기존 $p$보다 작은 차원인 $d$차원 부분 공간 subspace를 찾는 문제임
- 이를 어떻게 구하냐? data와 subspace로부터 수직거리를 최소화하여 구함
- 직선거리의 최소화? 제곱합 $A^{T}A$, $AA^{T}$ 을 최소화하는 것
- 특이값 분해는 원본 행렬 $A$보다 $A^{T}A$, $AA^{T}$를 다루는 것
특이값 이란?
$n \times p$ 행렬 $A$에 대해 $A^{T}A$의 고유값을 $\lambda_{1}, ... ,\lambda_{p}$라고 할 때, $\sigma_{1}= \sqrt{\lambda_{1}} , \sigma_{2}= \sqrt{\lambda_{2}} , ... , \sigma_{p}= \sqrt{\lambda_{p}} $를 행렬 $A$의 특이값 Singular value라고 함
따라서, 행렬 $A$의 특이값은 행렬 $A$를 제곱한 행렬의 고유값에 루트 씌운 값임
- 특이값 분해 공식 : $A = U \Sigma V^{T}$

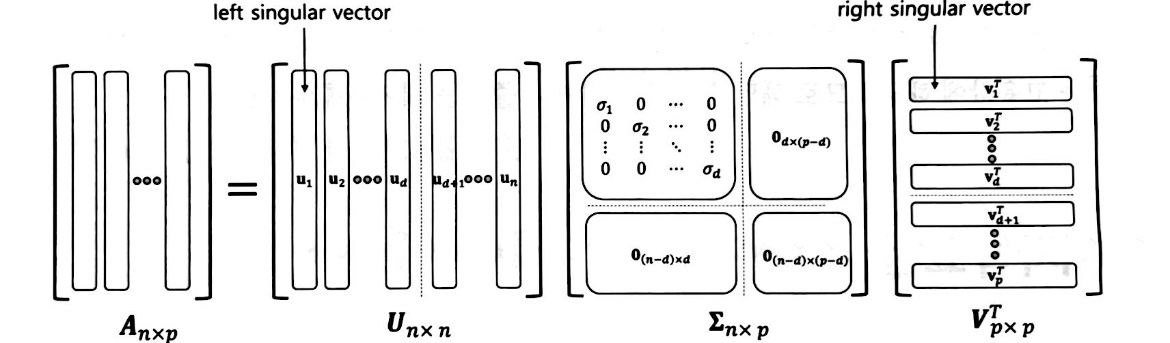
- 행렬 $U$의 열벡터 : $AA^{T}$의 고유벡터로 구성됨 left singular vector
- 행렬 $V$의 열벡터 : $A^{T}A$의 고유벡터로 구성됨 right singular vector
- $\Sigma$의 대각원소 : 행렬 $A$의 특이값

- 위 시각화를 보면 선형변환 $A$는 $U,\Sigma,V^{T}$ 총 3 단계의 변환을 거침
- $U, V^{T}$ : 고유벡터로 기존의 행렬을 회전하는 것
- $\Sigma$ 대각원소 : 고유값에 해당되므로 해당 영역을 늘리거나 줄이는 데 사용
728x90
'STUDY > 인공지능' 카테고리의 다른 글
| [머신러닝/딥러닝] feature importance(MDI, Drop Column, Permutation) 각 각에 대한 설명, 코드 (0) | 2023.07.16 |
|---|---|
| [ML 책] 차원 축소, 차원의 저주 (0) | 2023.06.27 |
| [ML 책] 고유값, 고유벡터, 고유값분해 (0) | 2023.06.22 |
| [ML 책] 스칼라, 벡터, 행렬, 텐서, 행렬 곱, 행렬 원소곱, 행렬식, 역행렬 (0) | 2023.06.20 |
| [ML 책] 지도 학습과 비지도 학습의 목적과 차이, 파라미터와 하이퍼 파라미터의 차이 (0) | 2023.06.20 |



